Clip Hình nào sau đây là hình vuông hình thang cân có một góc vuông 🆗
Mẹo Hướng dẫn Hình nào sau đây là hình vuông vắn hình thang cân có một góc vuông Mới Nhất
Bùi Mạnh Hùng đang tìm kiếm từ khóa Hình nào sau đây là hình vuông vắn hình thang cân có một góc vuông được Cập Nhật vào lúc : 2022-04-18 12:10:41 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Tải app VietJack. Xem lời giải nhanh hơn! Bài 1: Hình vuông là tứ giác có
A. Có bốn cạnh bằng nhau
B. Có bốn góc bằng nhau
C. Có 4 góc vuong và bốn cạnh bằng nhau
D. Cả A, B, C đều sai
Hiển thị đáp ánLời giải
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Đáp án cần chọn là: C
Bài 2: Điền cụm từ thích hợp nhất vào chỗ trống: “Tứ giác có 4 cạnh bằng nhau và 4 góc bằng nhau là …”
A. Hình vuông
B. Hình chữ nhật
C. Hình bình hành
D. Hình thoi
Hiển thị đáp ánLời giải
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Đáp án cần chọn là: A
Bài 3: Khẳng định nào sau đây là sai?
A. Hình vuông vừa là hình thoi vừa là hình chữ nhật
B. Hình vuông là hình chữ nhật nhưng không là hình thoi
C. Hình vuông có hai tuyến đường chéo bằng nhau và vuông góc với nhau
D. Hình vuông có đường chéo là phân giác những góc trong hình vuông vắn
Hiển thị đáp ánLời giải
Hình vuông vừa là hình chữ nhật và hình thoi nên nó có đầy đủ tính chất của hình chữ nhật và hình thoi.
Từ đó A, C, D đúng, B sai.
Đáp án cần chọn là: B
Bài 4: Nếu ABCD là hình vuông vắn thì:
A. AC = BD
B. AC, BD giao nhau tại trung điểm mỗi đường
C. AC ⊥ BD
D. Cả A, B, C đều đúng
Hiển thị đáp ánLời giải
Hình vuông có hai tuyến đường chéo bằng nhau, vuông góc với nhau và giao nhau tại trung điểm mỗi đường nên ABCD là hình vuông vắn thì AC = BD, AC ⊥ BD, AC và BD giao nhau tại trung điểm mỗi đường.
Đáp án cần chọn là: D
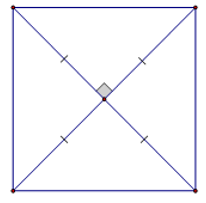
Bài 5: Hãy chọn câu đúng. Cho hình vẽ. Tứ giác là hình vuông vắn theo tín hiệu:
A. Hình thoi có một góc vuông
B. Tứ giác có hai tuyến đường chéo bằng nhau
C. Hình bình hành có hai tuyến đường chéo bằng nhau
D. Hình thoi có hai tuyến đường chéo bằng nhau
Hiển thị đáp ánLời giải
Từ hình vẽ ta thấy hai tuyến đường chéo của tứ giác vuông góc và giao nhau tại trung điểm mỗi đường nên nó là hình thoi.
Hình thoi này còn có hai tuyến đường chéo bằng nhau nên nó là hình vuông vắn.
Đáp án cần chọn là: D
Bài 6: Hãy chọn câu đúng. Cho hình vẽ. Tứ giác là hình vuông vắn theo tín hiệu:
A. Hình thoi có một góc vuông
B. Tứ giác có hai tuyến đường chéo bằng nhau
C. Hình bình hành có hai tuyến đường chéo bằng nhau
D. Hình thoi có hai tuyến đường chéo bằng nhau
Hiển thị đáp ánLời giải
Từ hình vẽ ta thấy bốn cạnh của tứ giác này bằng nhau nên tứ giác này là hình thoi.
Hình thoi này còn có một góc vuông nên nó là hình vuông vắn.
Đáp án cần chọn là: A.
Bài 7: Chọn câu vấn đáp đúng. Tứ giác nào có hai tuyến đường chéo vuông góc với nhau?
A. Hình thoi
B. Hình vuông
C. Hình chữ nhật
D. Cả A và B
Hiển thị đáp ánLời giải
+ Hình thoi và hình vuông vắn đều có hai tuyến đường chéo vuông góc với nhau.
Đáp án cần chọn là: D
Bài 8: Chọn câu sai. Tứ giác nào có hai tuyến đường chéo bằng nhau.
A. Hình vuông
B. Hình thang cân
C. Hình chữ nhật
D. Hình thoi
Hiển thị đáp ánLời giải
Trong những hình: hình vuông vắn, hình chữ nhật, hình thang cân, hình thoi thì hình thoi là hình có hai tuyến đường chéo không bằng nhau.
Đáp án cần chọn là: D
Bài 9: Cho hình vuông vắn ABCD. Trên những cạnh AB, BC, CD, DA lần lượt lấy những điểm E, F, G, H sao cho AE = BF = CG = DH sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình vuông
Hiển thị đáp ánLời giải
+ Vì ABCD là hình vuông vắn nên AB = BC = CD = DA (tính chất).
Mà AE = BF = CG = DH (gt) nên AB – AE = BC – BF = CD – CG = DA – DH hay DG = CF = EB = AH
Từ đó suy ra ΔAHE = ΔDGH = ΔCFG = ΔEBF (c-g-c) nên HG = GF = HE = EF.
Vì HG = GF = HE = EF nên tứ giác EFGH là hình thoi.
+ Vì ΔAHE = ΔBEF (cmt)
Hình thoi EFGH có 
nên EFGH là hình vuông vắn.
Đáp án cần chọn là: D
Bài 10: Cho hình thoi ABCD, O là giao điểm của hai tuyến đường chéo. Các tia phân giác 4 góc đỉnh O cắt những cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình vuông
Hiển thị đáp ánLời giải
+ Vì ABCD là hình thoi nên AC ⊥ BD; OA = OC; OB = OD (tính chất).
Mà OE; OF; OG; OH lần lượt là phân giác 
nên ta có:
Tương tự ta có: ΔOFB = ΔOHD (g – c – g) ⇒ OF = OH (2)
Từ (1) và (2) suy ra: tứ giác EFGH là hình bình hành vì có hai tuyến đường chéo EG; HF giao nhau tại trung điểm mỗi đường.
Lại xét ΔOEB và ΔOFB có:
Nên ΔOEB = ΔOFB (g – c – g) ⇒ OE = OF ⇒ 2OE = 2OF hay EG = HF
Suy ra: hình bình hành EFGH có hai tuyến đường chéo bằng nhau EG = HF nên EFGH là hình chữ nhật.
Hình chữ nhật EFGH có: EG ⊥ HF nên EFGH là hình vuông vắn.
Đáp án cần chọn là: D
Bài 11: Cho hình vuông vắn có chu vi 28 cm. Độ dài cạnh hình vuông vắn là:
A. 4cm
B. 7 cm
C. 14 cm
D. 8 cm
Hiển thị đáp ánLời giải
Hình vuông có 4 cạnh bằng nhau nên chu vi hình vuông vắn bằng 4a. (a là độ dài một cạnh)
Từ giả thiết ta có 4a = 28 ⇔ a = 7cm.
Vậy cạnh hình vuông vắn là a = 7cm
Đáp án cần chọn là: B
Bài 12: Cho hình vuông vắn có chu vi 32 cm. Độ dài cạnh hình vuông vắn là:
A. 10cm
B. 15 cm
C. 5 cm
D. 8 cm
Hiển thị đáp ánLời giải
Hình vuông có 4 cạnh bằng nhau nên chu vi hình vuông vắn bằng 4a. (a là độ dài một cạnh)
Từ giả thiết ta có 4a = 32 ⇔ a = 8cm.
Vậy cạnh hình vuông vắn là a = 8cm
Đáp án cần chọn là: D
Bài 13: Cho hình vuông vắn có chu vi 16 cm. Bình phương độ dài một đường chéo của hình vuông vắn là:
A. 32
B. 16
C. 24
D. 18
Hiển thị đáp ánLời giải
Gọi hình vuông vắn ABCD có chu vi là 16cm. Khi đó 4.AB = 16cm
⇒ AB = 4cm = AB = CD = DA
Xét tam giác ABC vuông tại B, theo định lý Pytago ta có
AB2 + BC2 = AC2 ⇒ AC2 = 42 + 42 ⇔ AC2 = 32
Vậy bình phương độ dài một đường chéo là: 32
Đáp án cần chọn là: A
Bài 14: Cho hình vuông vắn có chu vi 20 cm. Bình phương độ dài một đường chéo của hình vuông vắn là:
A. 32
B. 50
C. 25
D. 30
Hiển thị đáp ánLời giải
Gọi hình vuông vắn ABCD có chu vi là 20cm. Khi đó 4.AB = 20cm
⇒ AB = 5cm = AB = CD = DA
Xét tam giác ABC vuông tại B, theo định lý Pytago ta có
AB2 + BC2 = AC2 ⇒ AC2 = 52 + 52 ⇔ AC2 = 50
Vậy bình phương độ dài một đường chéo là: 50
Đáp án cần chọn là: B
Bài 15: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để hình bình hành EFGH là hình vuông vắn.
A. BD ⊥ AC; BD = AC
B. BD ⊥ AC
C. BD = AC
D. AC = BD và AB // CD
Hiển thị đáp ánLời giải
Ta có EH; EF lần lượt là đường trung bình của tam giác ABD; BAC nên 
(1)
Hình bình hành EFGH là hình vuông vắn khi và chỉ khi 
(2)
Từ (1); (2) ⇒ 
thì hình bình hành EFGH là hình vuông vắn
Đáp án cần chọn là: A
Bài 16: Cho hình vuông vắn ABCD. M là vấn đề nằm trong hình vuông vắn. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông vắn khi.
A. M trên đường chéo AC
B. M thuộc cạnh DC
C. M thuộc đường chéo BD
D. M tùy ý nằm trong hình vuông vắn ABCD
Hiển thị đáp ánLời giải
Tứ giác AFME có: 
nên AEMF là hình chữ nhật
Để hình chữ nhật AEMF là hình vuông vắn thì AM là phân giác 
Mà ta lại sở hữu: AC là phân giác 
(do ABCD là hình vuông vắn)
Nên suy ra M Є AC.
Đáp án cần chọn là: A
Bài 17: Cho hình vuông vắn ABCD. M, N, P, Q. là trung điểm những cạnh AB, BC, CD, DA. Hãy chọn câu đúng.
Lời giải
Gọi cạnh của hình vuông vắn ABCD là a.
Vì ABCD là hình vuông vắn là M, N, P, Q. là trung điểm những cạnh AB, BC, CD, DA nên ta có AM = MB = BN = NC = CP = PD = DQ = QA = a/2
Từ đó: ΔAQM = ΔBMN = ΔCPN = ΔDQP (c – g – c)
Lại có SABCD = a2.
Nên SMNPQ = SABCD – SAMQ – SMBN – SCPN – SDPQ = 
Vậy SMNPQ = (1/2)SABCD.
Đáp án cần chọn là: C
Bài 18: Cho hình vuông vắn ABCD cạnh 8 cm. M, N, P, Q. là trung điểm những cạnh AB, BC, CD, DA. Tính diện tích s quy hoạnh tứ giác MNPQ.
A. SMNPQ = 28 cm2
B. SMNPQ = 30cm2
C. SMNPQ = 16cm2
D. SMNPQ = 32cm2
Hiển thị đáp ánLời giải
Vì ABCD là hình vuông vắn và M, N, P, Q. là trung điểm những cạnh AB, BC, CD, CA nên ta có AM = MB = BN = NC = CP = PD = DQ = QA = 8/2 = 4 cm
Từ đó: ΔAQM = ΔBMN = ΔCPN = ΔDQP (c – g – c)
Suy ra 
Lại có SABCD = 82 = 64.
Nên SMNPQ = SABCD – SAMQ – SMBN – SCPN – SDPQ = 
Vậy SMNPQ = 32 cm2.
Đáp án cần chọn là: D
Bài 19: Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là những trung điểm của AB, BC, AC. Tam giác ABC nên phải có thêm điều kiện gì để hình chữ nhật AMNP là hình vuông vắn?
Lời giải
Hình chữ nhật AMNP là hình vuông vắn ⇔ AM = AP
Mà 
(gt) nên AM = AP ⇔ AB = AC
Vậy nếu tam giác ABC vuông cân tại A thì hình chữ nhật AMNP là hình vuông vắn.
Đáp án cần chọn là: B
Bài 20: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy những điểm H, G sao cho BH = HG = GC. Qua H và G kẻ những đường vuông góc với BC, chúng cắt AB và AC theo thứ tự tại E và F.
1. Tứ giác EFGH là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình vuông
Hiển thị đáp ánLời giải
Suy ra ΔFGC là tam giác vuông cân tại G ⇒ FG = GC
Chứng minh tương tự:
Xét tam giác vuông EHB có:
Suy ra tam giác EBH vuông cân tại H ⇒ EH = HB
Mà BH = HG = GC (gt) nên FG = EH = HG
Lại có: 
⇒ EFGH là hình bình hành (dhnb)
Mà 
= 900 (do EH ⊥ BC) nên hình bình hành EFGH là hình chứ nhật
Mặt khác EH = HG (cmt) nên hình chữ nhật EFGH là hình vuông vắn.
Đáp án cần chọn là: D
2. Cho BC = 9 cm. Tính chu vi của tứ giác EFGH.
A. 12 cm
B. 9 cm
C. 16 cm
D. 20 cm
Hiển thị đáp ánLời giải
Vì FG = EH = HG nên 
Do đó chu vi hình vuông vắn EFGH là 4.HG = 4.3 = 12 cm
Đáp án cần chọn là: A
Bài 21: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy những điểm H, G sao cho BH = HG = GC. Qua H và G kẻ những đường vuông góc với BC, chúng cắt AB và AC theo thứ tự tại E và F.
1. Chọn câu đúng nhất
A. EG =HF
B. EG ⊥ HF
C. FG = EG
D. Cả A, B, C đều đúng
Hiển thị đáp ánLời giải
Suy ra ΔFGC là tam giác vuông cân tại G ⇒ FG = GC
Chứng minh tương tự:
Suy ra tam giác EBH vuông cân tại H ⇒ EH = HB
Mà BH = HG = GC (gt) nên FG = EH = HG
Lại có: 
⇒ EH // FG (định lí từ vuông góc đến song song)
Xét tứ giác EFGH có 
⇒ Tứ giác EFGH là hình bình hành (dhnb)
Mà 
= 900 (do EH ⊥ BC) nên hình bình hành EFGH là hình chứ nhật
Mặt khác EH = HG (cmt) nên hình chữ nhật EFGH là hình vuông vắn.
Suy ra EG = HF; EG ⊥ HF.
Đáp án cần chọn là: D
2. Cho BC = 12 cm. Tính chu vi của tứ giác EFGH.
A. 12 cm
B. 9 cm
C. 16 cm
D. 20 cm
Hiển thị đáp ánLời giải
Vì FG = EH = HG nên 
Do đó chu vi hình vuông vắn EFGH là 4.HG = 4.4 = 16 cm
Đáp án cần chọn là: C
Bài 22: Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC. K là vấn đề đối xứng với M qua điểm I.
1. Tứ giác AKMB là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình vuông
Hiển thị đáp ánLời giải
+ Tam giác ABC cân tại A, AM là đường trung tuyến nên AM đồng thời là đường cao.
Suy ra tứ giác AMCK là hình bình hành (dhnb)
Lại có 
(cmt) nên hình bình hành AMCK là hình chữ nhật.
+ Ta có: AK // MC (do AMCK là hình chữ nhật), M Є BC (gt) ⇒ AK // BM
Mà BM = MC (do AM là trung tuyến), AK = MC (do AMCK là hình chữ nhật) nên AK – BM (tính chất bắc cầu)
Xét tứ giác ABMK có: 
Suy ra tứ giác ABMK là hình bình hành.
Đáp án cần chọn là: C
2. Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông vắn
A. Tam giác ABC vuông cân tại A
B. Tam giác ABC vuông cân tại B
C. Tam giác ABC đều
D. Tam giác ABC vuông cân tại C
Hiển thị đáp ánLời giải
Hình chữ nhật AMCK là hình vuông vắn ⇔ AM = MC
Do AM là đường trung tuyến của tam giác ABC nên AM = ½BC
⇔ tam giác ABC vuông tại A.
Vậy nếu tam giác ABC vuông cận tại A thì tứ giác AMCK là hình vuông vắn
Đáp án cần chọn là: A
Bài 23: Cho tam giác ABC vuông tại A. Điểm M thuộc BC. Qua M dựng đường thẳng song song với AB cắt AC tại D. Qua M dựng đường thẳng song song với AC cắt AB tại E.
1. Tứ giác ADME là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình vuông
Hiển thị đáp ánLời giải
Vì MD //AB; ME // AC mà AB ⊥ AC nên MD ⊥ AC; ME ⊥ AB.
Suy ra 
nên tứ giác DMEA là hình chữ nhật
Đáp án cần chọn là: A
2. Tìm vị trí điểm M để tứ giác ADME là hình vuông vắn.
A. M là chân đường phân giác của  xuống cạnh BC.
B. M là chân đường cao hạ từ đỉnh A xuống cạnh BC.
C. M là chân đường trung tuyến từ đỉnh A xuống cạnh BC.
D. Đáp án khác.
Hiển thị đáp ánLời giải
Hình chữ nhật ADME là hình vuông vắn ⇔ AM là phân giác 
Hay AM là phân giác góc BAC.
Đáp án cần chọn là: A
Bài 24: Cho hình cuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chọn câu đúng.
A. AK + CE = BE
B. AK + CE = 2BE
C. AK + CE = ½BE
D. AK + CE > BE
Hiển thị đáp ánLời giải
Trên tia đối của tia CD lấy điểm M sao cho CM = AK.
Ta có AK + CE = CM + CE = EM.
Ta cần chứng tỏ EM = BE
Suy ra: tam giác EBM cân tại E (định nghĩa tam giác cân).
⇒ BE = EM
⇒ AK + CE = CM +CE = EM = BE
⇒ AK + CE = BE
Đáp án cần chọn là: A
Xem thêm những bài tập trắc nghiệm Toán lớp 8 tinh lọc, có đáp án rõ ràng hay khác:
Xem thêm những loạt bài Để học tốt Toán lớp 8 hay khác:
- Giải bài tập Toán 8
Giải sách bài tập Toán 8
Top 75 Đề thi Toán 8 có đáp án
[embed]https://www.youtube.com/watch?v=ieCkGJwl-s8[/embed]
Giới thiệu kênh Youtube VietJack
Hỏi bài tập trên ứng dụng, thầy cô VietJack trả lời miễn phí! - Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 8 có đáp án
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Nhóm học tập facebook miễn phí cho teen 2k8: fb.com/groups/hoctap2k8/
Theo dõi chúng tôi miễn phí trên social facebook và youtube:Loạt bài Lý thuyết & 700 Bài tập Toán lớp 8 có lời giải rõ ràng có đầy đủ Lý thuyết và những dạng bài có lời giải rõ ràng được biên soạn bám sát nội dung chương trình sgk Đại số 8 và Hình học 8.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các phản hồi không phù phù phù hợp với nội quy phản hồi trang web sẽ bị cấm phản hồi vĩnh viễn.
[embed]https://www.youtube.com/watch?v=eyqrTS-m13c[/embed]