Video Triangle formed between two parallel lines ?
Thủ Thuật về Triangle formed between two parallel lines Mới Nhất
Lã Hiền Minh đang tìm kiếm từ khóa Triangle formed between two parallel lines được Update vào lúc : 2022-10-05 02:55:24 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.You may use the facts, formulas, and theorems below in your solutions unless you are being asked to derive the formula or a special case, explain why the theorem or a special case is true, etc. If you think there is something I have left off this list that is needed to solve a problem, please ask me
Nội dung chính- Video lessonVideo lessonWhat does it mean when two lines are parallel in a triangle?When two triangles are situated between two parallel lines are they the same?What angles are formed between the two parallel lines?How do you solve a triangle with parallel lines?
When two lines intersect they form two pairs of opposite angles, A + C and B + D. Another word for opposite angles are vertical angles.
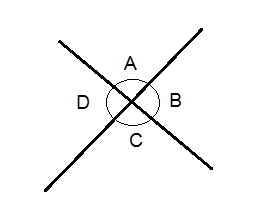
Vertical angles are always congruent, which means that they are equal.
Adjacent angles are angles that come out of the same vertex. Adjacent angles share a common ray and do not overlap.

The size of the angle xzy in the picture above is the sum of the angles A and B.
Two angles are said to be complementary when the sum of the two angles is 90°.
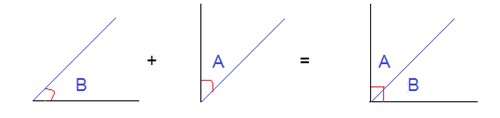
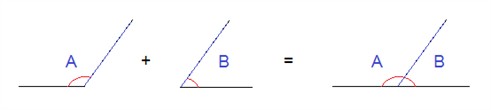
Two angles are said to be supplementary when the sum of the two angles is 180°.
If we have two parallel lines and have a third line that crosses them as in the ficture below - the crossing line is called a transversal
When a transversal intersects with two parallel lines eight angles are produced.
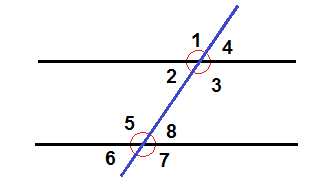
The eight angles will together form four pairs of corresponding angles. Angles 1 and 5 constitutes one of the pairs. Corresponding angles are congruent. All angles that have the same position with regards to the parallel lines and the transversal are corresponding pairs e.g. 3 + 7, 4 + 8 and 2 + 6.
Angles that are in the area between the parallel lines like angle 2 and 8 above are called interior angles whereas the angles that are on the outside of the two parallel lines like 1 and 6 are called exterior angles.
Angles that are on the opposite sides of the transversal are called alternate angles e.g. 1 + 8.
All angles that are either exterior angles, interior angles, alternate angles or corresponding angles are all congruent.
Example
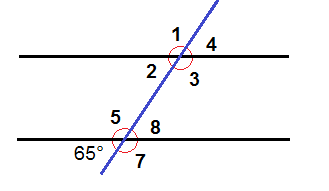
The picture above shows two parallel lines with a transversal. The angle 6 is 65°. Is there any other angle that also measures 65°?
6 and 8 are vertical angles and are thus congruent which means angle 8 is also 65°.
6 and 2 are corresponding angles and are thus congruent which means angle 2 is 65°.
6 and 4 are alternate exterior angles and thus congruent which means angle 4 is 65°.
Video lesson
Find the measure of all the angles in the figure
[embed]https://www.youtube.com/watch?v=Pfhb-jnDtPo[/embed]
Two lines that are stretched into infinity and still never intersect are called coplanar lines and are said to be parallel lines. The symbol for "parallel to" is //.
If we have two lines (they don't have to be parallel) and have a third line that crosses them as in the figure below - the crossing line is called a transversal:
In the following figure:
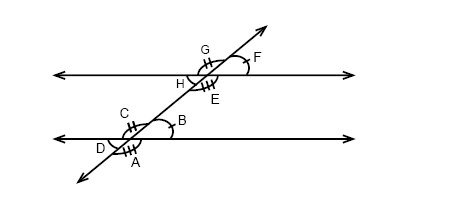
If we draw to parallel lines and then draw a line transversal through them we will get eight different angles.
The eight angles will together form four pairs of corresponding angles. Angles F and B in the figure above constitutes one of the pairs. Corresponding angles are congruent if the two lines are parallel. All angles that have the same position with regards to the parallel lines and the transversal are corresponding pairs.
Angles that are in the area between the parallel lines like angle H and C above are called interior angles whereas the angles that are on the outside of the two parallel lines like D and G are called exterior angles.
Angles that are on the opposite sides of the transversal are called alternate angles e.g. H and B.
Angles that share the same vertex and have a common ray, like angles G and F or C and B in the figure above are called adjacent angles. As in this case where the adjacent angles are formed by two lines intersecting we will get two pairs of adjacent angles (G + F and H + E) that are both supplementary.
Two angles that are opposite each other as D and B in the figure above are called vertical angles. Vertical angles are always congruent.
$$angle A; angle F; angle G; angle D;are; exterior; angles\ angle B; angle E; angle H; angle C;are; interior; angles\ angle B;and; angle E,; angle H;and; angle C;are; consecutive; interior; angles\ angle A;and; angle G,; angle F;and; angle D;are; alternate; exterior; angles\ angle E;and; angle C,; angle H;and; angle B;are; alternate;interior; angles\ left.beginmatrix angle A;and; angle E,; angle C;and; angle G\ angle D;and; angle H,; angle F;and; angle B\ endmatrixright} ;are; corresponding; angles$$
Two lines are perpendicular if they intersect in a right angle. The axes of a coordinate plane is an example of two perpendicular lines.
In algebra 2 we have learnt how to find the slope of a line. Two parallel lines have always the same slope and two lines are perpendicular if the product of their slope is -1.
Video lesson
Find the value of x in the following figure

[embed]https://www.youtube.com/watch?v=fRihRLaR0mY[/embed]
What does it mean when two lines are parallel in a triangle?
If a line parallel to one side of a triangle intersects the other two sides, then it divides the two sides proportionally. The converse is also true. In the image below, this tells us AD / DB = AE / EC.When two triangles are situated between two parallel lines are they the same?
Triangles between two parallel lines have the same height.What angles are formed between the two parallel lines?
The parallel lines never intersect, hence no angle is formed between two parallel lines.How do you solve a triangle with parallel lines?
If a line parallel to one side of a triangle intersects the other two sides of the triangle, then the line divides these two sides proportionally. If ¯DE∥¯BC , then ADDB=AEEC . Tải thêm tài liệu liên quan đến nội dung bài viết Triangle formed between two parallel lines Parallel Triangle Calculator Triangle Proportionality Theorem Similar triangles